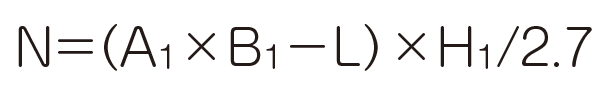国交省からの改正基準法に対するマニュアルで、先日、公開された「2024年9月第2版」で、衝撃的な変更があった「N値計算」。それをブログテーマにする#2ですw
さて、そもそも論、N値計算とは?って部分で、日常的に業務で使っていると、式の扱いは理解しているけど、その実はどうだろう?っていうと意外と知らなかったりします。ちょっとそれらを紐解いていくことにします。
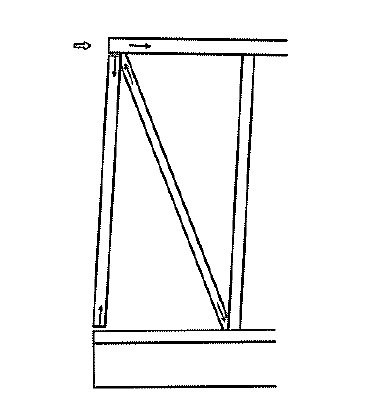
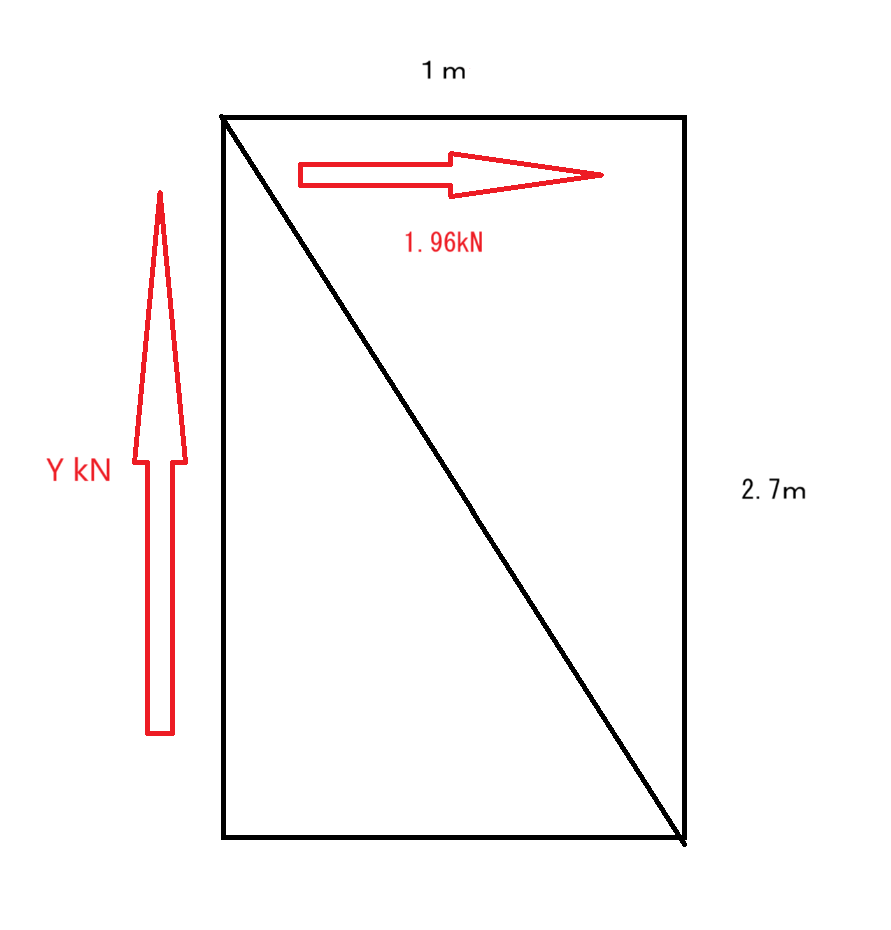
地震などで建物に水平力がかかるとき、それをつっかえ棒のように「筋交い等」で受けると、変形しなくなりますが、その水平力がすごく大きいときには、筋交いはちゃんと受けていても、図のような力の作用状態になることで、柱が浮いて引き抜かれる状況が発生します。これを「柱のほぞ抜け」といいます。
柱が引き抜かれれば、どんなに筋交いが踏ん張っていたとしても、上部の梁からの力を基礎まで伝達できなくなりますので、建物は瓦解してしまいます。この被害が顕著に表れたのが「平成7年阪神・淡路大震災」です。
そこで、国は、平成10年に「建築基準法の一部を改正する法律(平成10年法律第100号)」を公布し、平成12年6月から施行するように、法律を改正し、この「柱のほぞ抜け」問題に、法的に対応させる措置をとりました。これが、
◎建築基準法第47条
(構造耐力上主要な部分である継手又は仕口)
第47条 構造耐力上主要な部分である継手又は仕口は,ボルト締,かすがい打,込み栓打その他の国土交通大臣が定める構造方法によりその部分の存在応力を伝えるように緊結しなければならない。この場合において,横架材の丈が大きいこと,柱と鉄骨の横架材とが剛に接合していること等により柱に構造耐力上支障のある局部応力が生ずるおそれがあるときは,当該柱を添木等によつて補強しなければならない。
2 前項の規定によるボルト締には,ボルトの径に応じ有効な大きさと厚さを有する座金を使用しなければならない。
◎告示 平12建告第1460号 木造の継手及び仕口の構造方法を定める件
です。ここでは、柱の引抜力に対しての対応だけではなく、筋交いの端部や、横架材の接合部などの規定も盛り込まれ、地震時の水平力が作用した場合でも、最後まで、接合箇所が壊れることがないような措置をとることを義務付けました。
ちょっと余談になりますが、耐震性については、実は、ひそかに懸念されていることがあって、それは、この平成12年、西暦2000年6月以前の木造建築物においては、この継手、仕口に対しての金物補強、あるいは、引抜についての検定が義務化されていませんので、新耐震基準で建築されていたとしても、大地震による倒壊の危険性があるというものです。これを「耐震性の2000年問題」といいます。
さて、この法改正で制定された「ほぞ抜け」に対する対策としては、「告示 平12建告第1460号」に記載されている、「ほぞの引き抜き」に対応するための金物の仕様を、柱が配置されている場所の条件から、告示に記載されている表第1~3から選択して設置するというもので、これが「告示第二号表1から表3までによる場合」という位置づけになります。
ところが、この告示には「N値計算」なるものの記載はありませんwww 言い換えますと、N値計算は、法的な規制を受けてできた法律上の算定式ではありません。この「N値計算」が紹介されたのは、平成12年に施行される法改正の講習会テキスト「平成12年6月1日施工 改正建築基準法(2年目施工)の解説 」で登場しました。

もう20年前のテキストですので、オークション等で手に入れるしかありませんが、この本の、
第2編 第1章 構造強度関係の基準の見直し P153~
で、登場します。

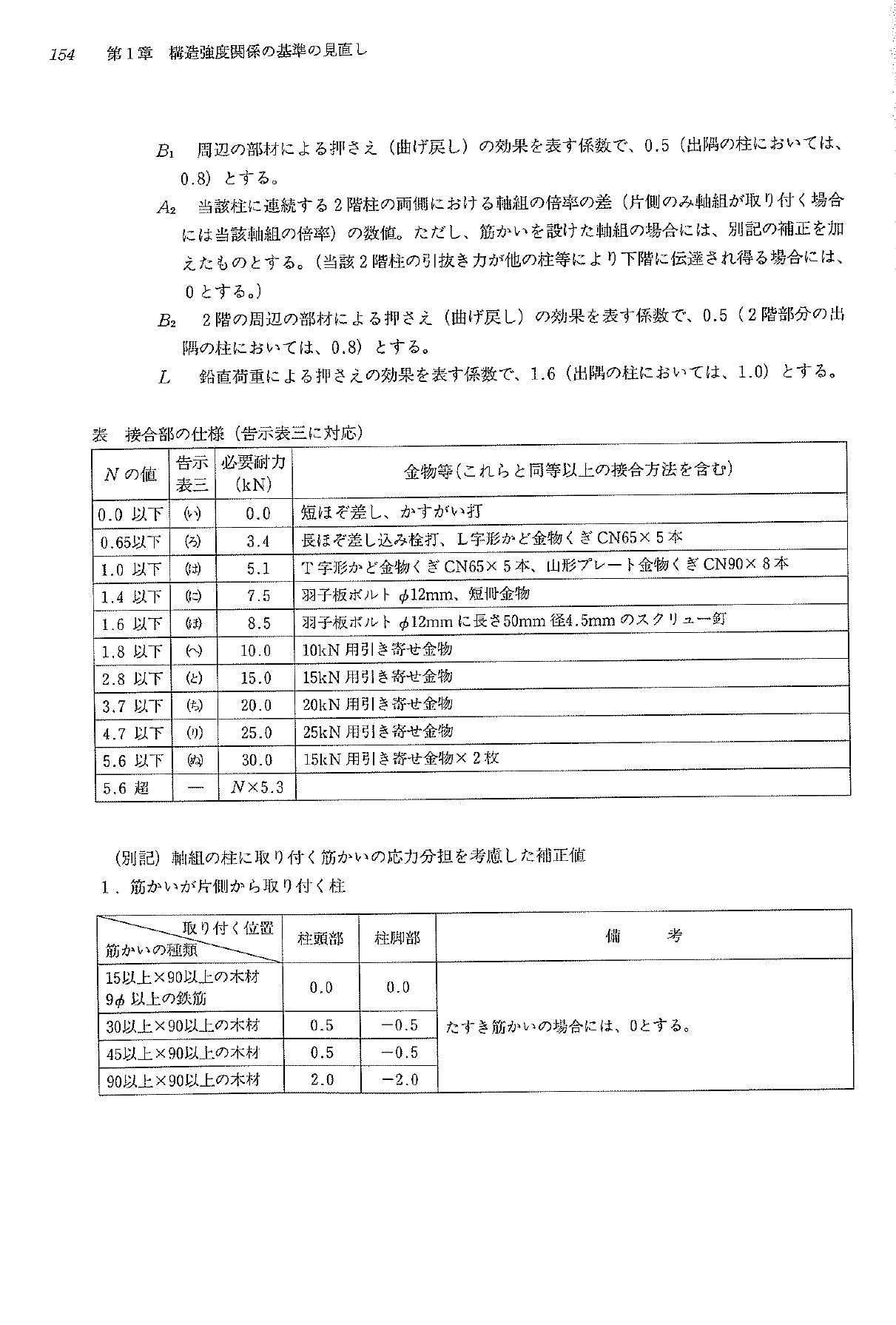

ところが、この講習会テキストで記載されている文言をそのまま書きますと、
告示中、表一及び表二は軸組の端部に取り付く柱に限定されており、中柱や例示以外の倍率の軸組を設けた場合等、これに当てはまらない部位については、次節4.を参照のこと。
となっています。次節4.は、N値計算の説明部分です。要するに「筋交い部分の柱は告示の表を使え、それ以外は計算で求めよ」という感じでの解説ですが、実は、この通りに計画すると、特に隅角部の柱は、ほぼホールダウン金物の設置が必要となり、当時は、ビス止め金物のホールダウン金物はまだ出回っていなかったため、柱にボルト穴を数本あけてホールダウン金物を取り付けるというもので、柱の根本の欠損はかなり大きくなるという指摘もありました。
よって、全体をこの「N値計算」で算出することも法的な運用レベルで認めたという流れになります。本来、引抜力の計算は、建物重量と地震力などをしっかりと加味し、筋交いなどの耐力壁の存在によってどのような力の作用があるかを計算しなければ算出できません。そこで、厳密、詳細な計算でなくとも、ある程度、簡易な計算で引抜力を算定できないか?と考え出されたものが「N値計算」というものです。
実務レベルでは、「告示の表を使うより金物ランクを落とせる」ということで歓迎された「N値計算」ですが、おそらく、この時に、N値計算の式そのものの解説が資料としてほとんどなかったために、単なる式の運用レベルでしか理解がなされず、今に至っていると思います。
そこで、次回は、N値計算の「式」そのものについて触れたいと思います。